中編で紹介した分子の重ね合わせの計算方法を実際にC++プログラムを組んでみます。OpenBabelの機能や応用と言うよりかは線型代数の計算がメインなので、C++で行列を扱う方法についても言及したいと思います。
計算対象
今回の計算例は適当に3次元化したドネペジルを、PDBの共結晶構造(6O4W)にあるドネペジルに重ねる計算をします。イメージとしては下図のような感じです。このとき重ねる母核はインダノンを指定することとします。橙色の分子が動かす方の分子で、灰色の分子が結晶構造の参照する分子です。
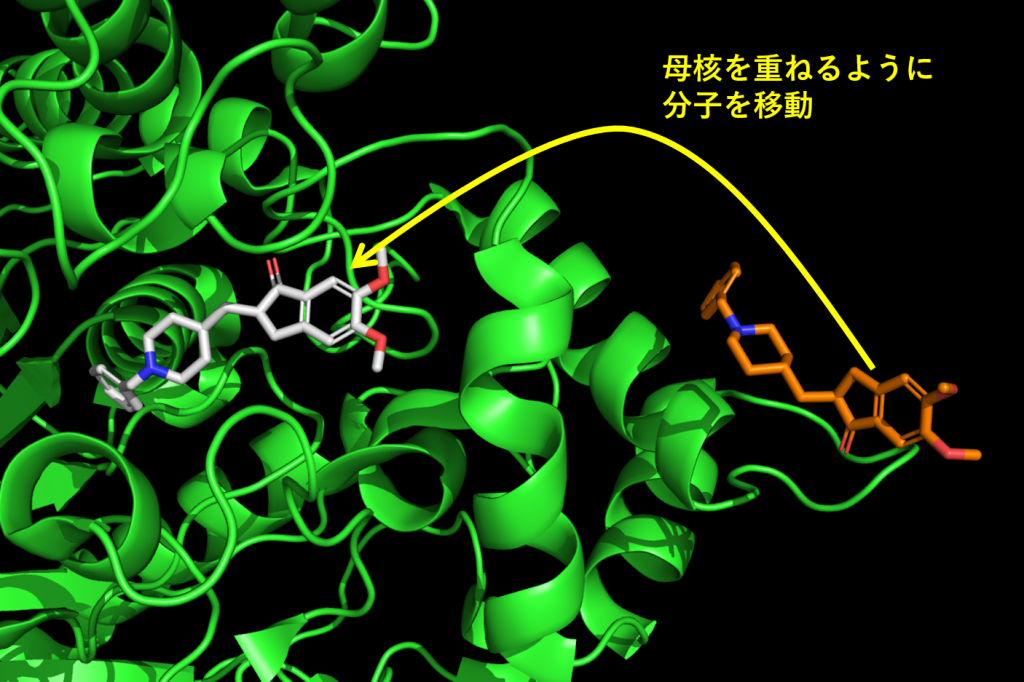
適当に発生させたコンホメーションなので結晶構造に重ね合わせると、タンパク質のアミノ酸側鎖などに衝突する可能性があります。しかしながら今回の目的は重ねることに主眼を置き、タンパク質との相互作用などは今回は考慮しないこととして、これらは後のブログで取り扱うこととします。
プログラム解説
今回のプログラムとデータをまとめたZIPファイルはここからダウンロードしてください。
このプログラムの実行方法ですが、先ず以下のコマンドを実行してEigenというライブラリをインストールしてください。Ubuntuの場合は以下のコマンドで、
$ sudo apt install -y libeigen3-devCentOSの場合は以下のコマンドです。
$ sudo yum -y install eigen3-develプログラムのコンパイル方法は以下の通りです。
$ g++ -std=c++11 MolSuperposition.cpp \
-I${HOME}/anaconda3/envs/ob3/include/openbabel3 \
-I/usr/include/eigen3 \
-L${HOME}/anaconda3/envs/ob3/lib \
-Wl,-rpath=${HOME}/anaconda3/envs/ob3/lib -l openbabela.outというファイルが出来ていれば成功です。プログラムの実行は以下のコマンドです。
$ ./a.outこのブログで扱うプログラムがだんだん長くなってきて全部を掲載出来なくなってきました。C++プログラムのコードを2つに分割して解説したいと思います。先ずは前半の部分を示します。
1 #include <fstream>
2 #include <iostream>
3 #include <string>
4
5 #include <openbabel/mol.h>
6 #include <openbabel/obconversion.h>
7 #include <openbabel/forcefield.h>
8 #include <openbabel/parsmart.h>
9 #include <openbabel/generic.h>
10
11 #include <Eigen/Dense>
12
13 using namespace std;
14 using namespace OpenBabel;
15 using namespace Eigen;
16
17 bool Superpose(OBMol& mol, OBMol& ref, string smarts);
18
19 int main(int argc, char* argv[]) {
20 // 力場の設定
21 string ff = "MMFF94";
22 OBForceField* pFF = OBForceField::FindForceField(ff);
23 if (!pFF) {
24 cerr << "指定の力場が見つかりませんでした" << endl;
25 return -1;
26 }
27 pFF->SetLogFile(&cout);
28 pFF->SetLogLevel(OBFF_LOGLVL_NONE);
29
30 // ファイルオープン
31 ifstream ifs1("Donepezil.sdf");
32 if (ifs1.fail()) {
33 cerr << "ファイルが見つかりませんでした" << endl;
34 return -1;
35 }
36
37 ifstream ifs2("template.sdf");
38 if (ifs2.fail()) {
39 cerr << "ファイルが見つかりませんでした" << endl;
40 return -1;
41 }
42
43 // 参照分子の読み込み
44 OBConversion conv;
45 conv.SetInAndOutFormats("SDF", "SDF");
46 OBMol mol, ref;
47 conv.Read(&mol, &ifs1);
48 conv.Read(&ref, &ifs2);
49 ifs1.close();
50 ifs2.close();
51
52 // 2分子の重ね合わせ計算
53 Superpose(mol, ref, "O=C1CCc2c1cccc2");
54
55 ofstream ofs("out.sdf");
56 conv.Write(&mol, &ofs);
57 ofs.close();
58
59 return 0;
60 }先ず線型代数の計算をするために、11行目に#include <Eigen/Dense>と記述しています。これはEigen(https://eigen.tuxfamily.org/index.php?title=Main_Page)というC++用の線型代数ライブラリです。線型代数用のライブラリで有名なものはやはりLAPACK/BLASでしょう。このLAPACK/BLASは何処のスーパーコンピュータにも最適化されたものが必ずインストールされています。ただ、元々FORTRAN用に作成されたもので、C++での使い勝手はイマイチで、古臭い感じです。スーパーコンピュータで動かすプログラムはLAPACK/BLASを利用すべきなのでしょうが、Eigenは非常に使いやすく出来ていて、私は良く利用します。この記事ではEigenの詳しい使い方には言及しませんが、いつか紹介できればと思います。
31行目で動かす方の分子のファイルを開いており、37行目では参照分子のファイルを開いています。53行目で分子の重ね合わせ計算をする関数を呼び出しているのですが、今回のブログのテーマは全てこの関数に詰め込んでいます。
それでは後半部分を見ていきましょう。
62 bool Superpose(OBMol& mol, OBMol& ref, string smarts) {
63 // 母核構造のマッチング
64 OBSmartsPattern smp;
65 smp.Init(smarts);
66 smp.Match(mol);
67 vector<vector<int> > ml_mol = smp.GetUMapList();
68 smp.Match(ref);
69 vector<vector<int> > ml_ref = smp.GetUMapList();
70
71 // 母核中心座標の計算
72 Vector3d cm = Vector3d::Zero(3);
73 Vector3d cr = Vector3d::Zero(3);
74 for (int i = 0; i < ml_mol[0].size(); i++) {
75 OBAtom* a_mol = mol.GetAtom(ml_mol[0][i]);
76 cm(0) += a_mol->x();
77 cm(1) += a_mol->y();
78 cm(2) += a_mol->z();
79 OBAtom* a_ref = ref.GetAtom(ml_ref[0][i]);
80 cr(0) += a_ref->x();
81 cr(1) += a_ref->y();
82 cr(2) += a_ref->z();
83 }
84 cm /= (double)(ml_mol[0].size());
85 cr /= (double)(ml_mol[0].size());
86
87 // 2分子の母核中心を原点へ移動
88 for (auto ii = mol.BeginAtoms(); ii != mol.EndAtoms(); ii++) {
89 double x = (*ii)->x() - cm(0);
90 double y = (*ii)->y() - cm(1);
91 double z = (*ii)->z() - cm(2);
92 (*ii)->SetVector(x, y, z);
93 }
94 for (auto ii = ref.BeginAtoms(); ii != ref.EndAtoms(); ii++) {
95 double x = (*ii)->x() - cr(0);
96 double y = (*ii)->y() - cr(1);
97 double z = (*ii)->z() - cr(2);
98 (*ii)->SetVector(x, y, z);
99 }
100
101 // 行列の計算
102 MatrixXd M = MatrixXd::Zero(4, 4);
103 for (int i = 0; i < ml_mol[0].size(); i++) {
104 OBAtom* a_mol = mol.GetAtom(ml_mol[0][i]);
105 double x = a_mol->x();
106 double y = a_mol->y();
107 double z = a_mol->z();
108 OBAtom* a_ref = ref.GetAtom(ml_ref[0][i]);
109 double x0 = a_ref->x();
110 double y0 = a_ref->y();
111 double z0 = a_ref->z();
112 M(0, 0) += -x * x0 - y * y0 - z * z0;
113 M(1, 0) += z * y0 - y * z0;
114 M(1, 1) += -x * x0 + y * y0 + z * z0;
115 M(2, 0) += x * z0 - z * x0;
116 M(2, 1) += -x * y0 - y * x0;
117 M(2, 2) += x * x0 - y * y0 + z * z0;
118 M(3, 0) += y * x0 - x * y0;
119 M(3, 1) += -x * z0 - z * x0;
120 M(3, 2) += -y * z0 - z * y0;
121 M(3, 3) += x * x0 + y * y0 - z * z0;
122 }
123
124 // 行列の対角化
125 SelfAdjointEigenSolver<MatrixXd> es(M);
126 if (es.info() != Success) exit(0);
127 VectorXd E;
128 MatrixXd V;
129 E = es.eigenvalues();
130 V = es.eigenvectors();
131
132 // 四元数から回転行列を計算
133 Matrix3d R;
134 double q0 = V(0, 0);
135 double q1 = V(1, 0);
136 double q2 = V(2, 0);
137 double q3 = V(3, 0);
138 R(0, 0) = q0 * q0 + q1 * q1 - q2 * q2 - q3 * q3;
139 R(1, 0) = 2 * (q0 * q3 + q1 * q2);
140 R(2, 0) = 2 * (q1 * q3 - q0 * q2);
141 R(0, 1) = 2 * (q1 * q2 - q0 * q3);
142 R(1, 1) = q0 * q0 - q1 * q1 + q2 * q2 - q3 * q3;
143 R(2, 1) = 2 * (q2 * q3 + q0 * q1);
144 R(0, 2) = 2 * (q0 * q2 + q1 * q3);
145 R(1, 2) = 2 * (-q0 * q1 + q2 * q3);
146 R(2, 2) = q0 * q0 - q1 * q1 - q2 * q2 + q3 * q3;
147
148 // 分子の回転と並進
149 for (auto ii = mol.BeginAtoms(); ii != mol.EndAtoms(); ii++) {
150 Vector3d X;
151 X(0) = (*ii)->x();
152 X(1) = (*ii)->y();
153 X(2) = (*ii)->z();
154 X = R * X; // 回転
155 X = X + cr; // 並進
156 (*ii)->SetVector(X(0), X(1), X(2));
157 }
158
159 return true;
160 }先ず、分子の母核部分を特定するために63~69行目で部分構造検索を行って原子インデックスを取得しています。動かす方の分子の原子リストはml_molという変数で、参照分子の方の原子リストはml_refという変数に入れています。どちらも1通りしかヒットしないことが分かっているので、ml_mol[0]のみ参照すれば良いことになります。分子の重ね合わせの計算は、回転する前に一旦原点へ回転中心を移動させる必要があります。上記プログラムの71~99行目はその原点への移動を行っています。101~122行目では分子を重ねる回転を表す四元数を求めるための\(4 \times 4\)行列を計算しています。124~130行目では行列を対角化して固有値と固有ベクトルを計算しています。今回は固有値は使っていないので129行目は無くてもよいです。132~146行目では四元数\(q=q_{0}+q_{1}i+q_{2}j+q_{3}k\)から回転行列を構成しています。最後に148~157行目では分子を回転させて、参照分子の位置へ移動させています。実はEigenというライブラリには四元数を扱えるQuaterniondというクラスが提供されています。このクラスを利用すれば、132~146行目で行っているような3次元の回転行列の計算は必要ありません。このQuaterniondクラスを利用する場合は132~157行目を以下のように書き換えてください。
Quaterniond Q(V(0, 0),V(1, 0),V(2, 0),V(3, 0));
Matrix3d R=Q.toRotationMatrix();
// 分子の回転と移動
for (auto ii = mol.BeginAtoms(); ii != mol.EndAtoms(); ii++) {
Vector3d X;
X(0) = (*ii)->x();
X(1) = (*ii)->y();
X(2) = (*ii)->z();
X = Q * X;
X = X + cr;
(*ii)->SetVector(X(0), X(1), X(2));
}計算結果
上記プログラムを実行するとout.sdfというSDファイルが出力されます。結晶構造(PDBID:6O4W)と出力されたSDファイルを重ね合わせた図は以下のようになります。母核として設定したインダノン部分がピッタリと重なっていることが分かります。
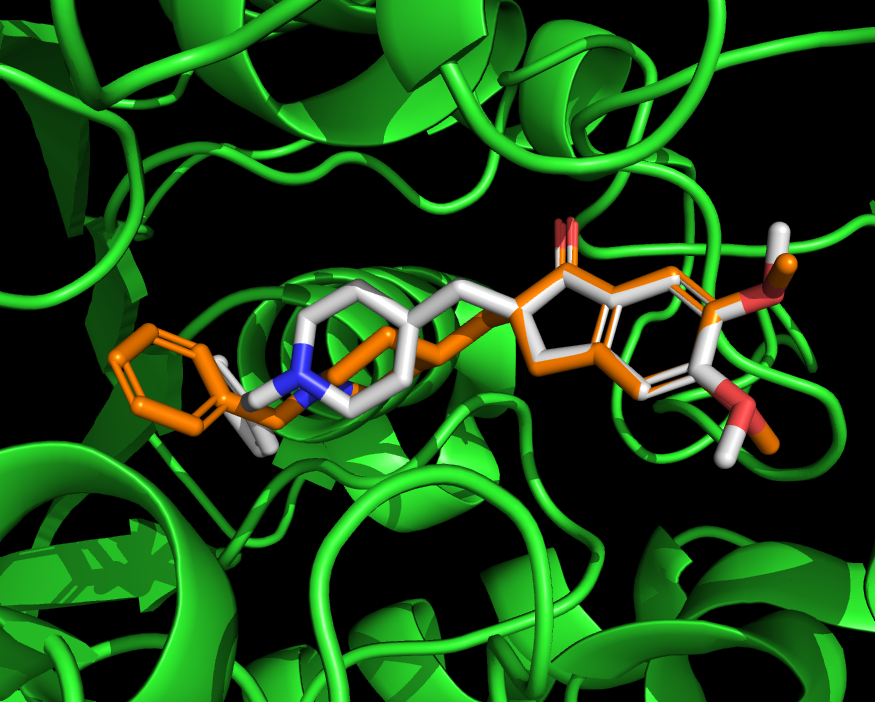
偶然でしょうが、見た感じ重ねた分子はタンパク質とはぶつかっていないように見えます。
Category: OpenBabel, プログラミング関連